What Are Graphs?
                         Graphs are a pervasive Data Structure in computer science ,before other details we formally define a graph.
 Graphs
                            A Graph is a set of vertices and edges which connect them,we write
                                                           G = {V,E}
                                        Where V is the set of vertices and E is the set of edges,
                                                         E = {(Vi,Vj)}
                                     Where Vi and Vj are in V.
Types of Graphs
               Directed Graphs
                                                        The edges has a  direction associated with them.
                                                        There are one or two edges associated between two nodes
              Undirected Graphs
                                                      The edges are non-directional.
                                                      There exists only one edge between two nodes .
              Weighted Graphs
                                                     Each edge has an associated weight.
              Unweighted Graphs
                                                     Edges donot have weight associated with them.
 Paths
                     A path ,P of length,K through a graph is a sequence of connected vertices:
                                             P = <V0,V1........Vk>
                               Where ,for all i in (0,K-1).

 
Representantion of Graph

                                 There are two ways of  reperenting a Graph  G = (V,E): as a collection of adjacency lists or as anadjacency matrix . the adjacency list representation is generally preferred ,as it provide a compact way to represent Sparse graphs-those for which edges are much less than vertices whereas adjacency matrix representation isPreffered in the dense Graphs-those for which number of edges is close to number of vertices.See Below the representation of two kinds of graphs,Note that in adjacency list representation for a undirected graph each EDGE is repeated since <u,v> is same as <v,u> for the case of a undirected graph more over the adjacency matrix is diagonally symmetric .

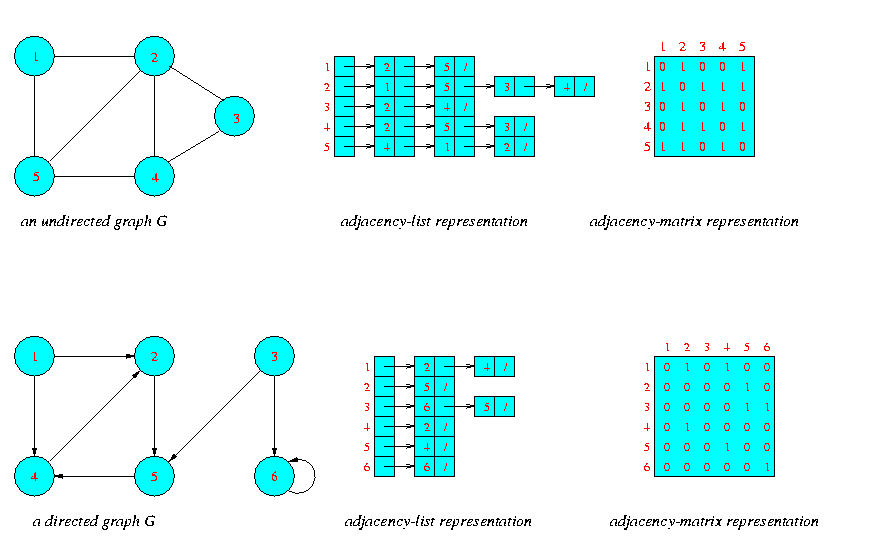
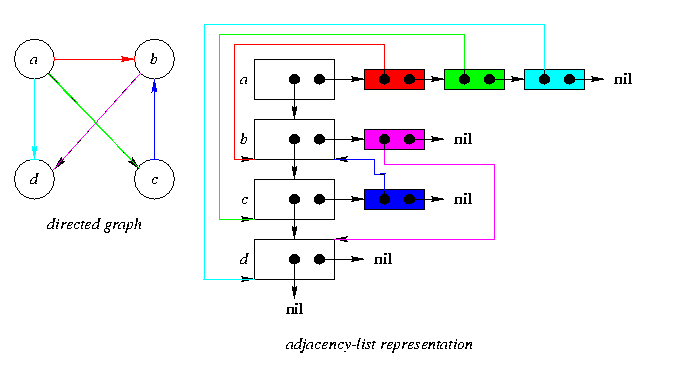
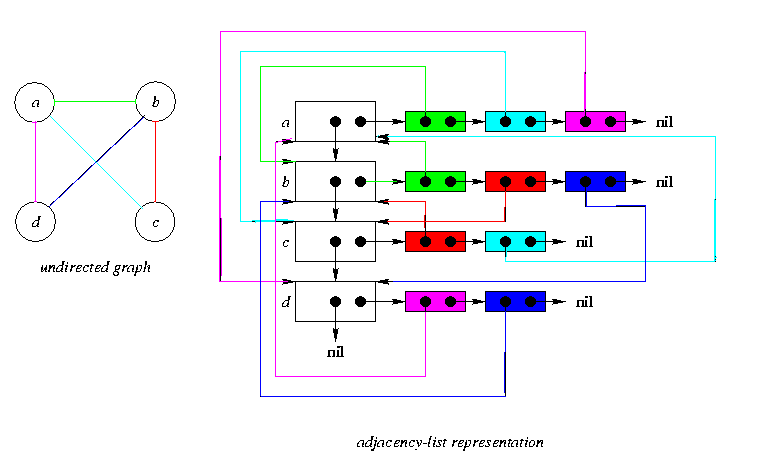
                               Whether a graph is directed or undirected ,the adjacency -list representation requires  O(V+E) memory.To represent a WEIGHTED GRAPH  each edge has a weight associated with it  ,the weight of the edge (u,v) in E is simply stored with vertex v in u's adjacency - list.The major drawback of this representation is that there is no quick way of finding a given edge.

                      For the ADJACENCY MATRIX representation  of a graph G=(V,E),we assume that the vaertices are numbered in some arbitary manner.The adjacency matrix representation of a graph G then consists of a |V| by |V| matrix such that

                                     aij  =  |    1 if(i,j) belong to E,
                                                       |    0  if (i,j) does not belong to E
                            Adjacency matrix reprentation of directed and undirected graphs are shown below,the adjacency matrix of a graph requires memory of the order V square, independent of the number of edges.To represent the weighted graphs we add weight w(u,v) of the edge E(u,v) as the entry in row u and column v of the adjacency matrix.if the edge doesnot exists ,a NIL value can be stored as its corresponding entry
 
 
 

                                                                                           Representation of a graph

Data Structure Required to strore the graph
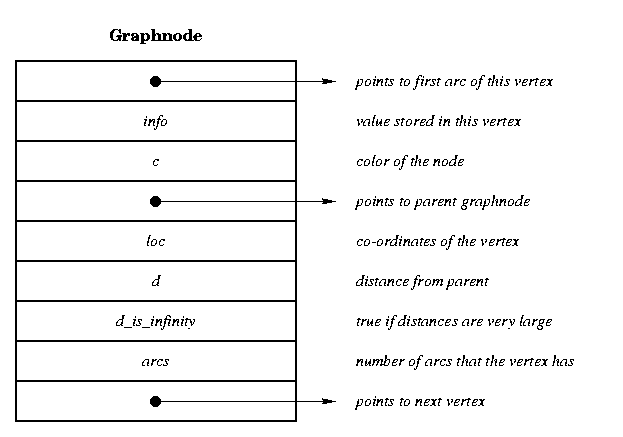
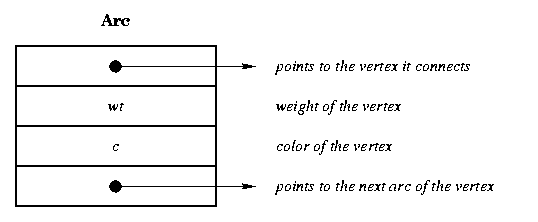
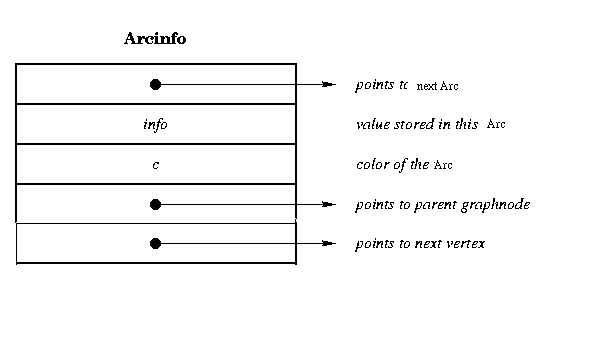
                           We require two Objects for the adjacency representation of Graphs ,one for representing the Vertices and other for representing the Edges ,the fundamental field present in the two are as follows.

                          
Keys to Home
    Graph Algorithms
  The Tutorial was written by Abhishek Goyal,Marghoob Mohiyuddin,Pooja Nath and Ruchi Saran		 Please email comments to:
[email protected] [email protected]
© Abhishek Goyal , 1999